ST_IsSimple
Signature
BOOLEAN ST_IsSimple(GEOMETRY geom);Description
Returns true if geom is simple.
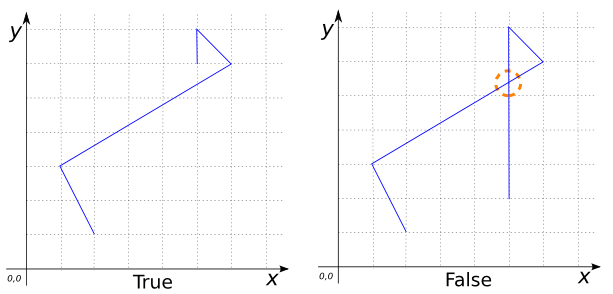
The SFS definition of simplicity follows the general rule that a Geometry is simple if it has no points of self-tangency, self-intersection or other anomalous points.
Simplicity is defined for each Geometry subclass as follows:
- Valid polygonal geometries are simple, since their rings must not self-intersect.
- Linear rings have the same semantics.
- Linear geometries are simple iff they do not self-intersect at points other than boundary points.
- Zero-dimensional geometries (points) are simple iff they have no repeated points.
- Empty Geometries are always simple.
Implements the OpenGIS Simple Features Implementation Specification for SQL version 1.2.1.
Examples
SELECT ST_IsSimple('POLYGON((0 0, 10 0, 10 6, 0 6, 0 0),
(1 1, 2 1, 2 5, 1 5, 1 1),
(8 5, 8 4, 9 4, 9 5, 8 5))');
-- Answer: TRUE
SELECT ST_IsSimple('MULTILINESTRING((0 2, 3 2, 3 6, 0 6, 0 2),
(5 0, 7 0, 7 1, 5 1, 5 0))');
-- Answer: TRUE
SELECT ST_IsSimple('GEOMETRYCOLLECTION(
MULTIPOINT((4 4), (1 1), (1 0), (0 3)),
LINESTRING(2 6, 6 2),
POLYGON((1 2, 4 2, 4 6, 1 6, 1 2)))');
-- Answer: TRUE
SELECT ST_IsSimple('LINESTRING(2 1, 1 3, 6 6, 5 7, 5 6)');
-- Answer: TRUE
SELECT ST_IsSimple('LINESTRING(2 1, 1 3, 6 6, 5 7, 5 2)');
-- Answer: FALSE