ST_GraphAnalysis
Signatures
-- Creates two tables:
-- INPUT_EDGES_NODE_CENT[NODE_ID, BETWEENNESS, CLOSENESS]
-- INPUT_EDGES_EDGE_CENT[EDGE_ID, BETWEENNESS]
ST_GraphAnalysis('INPUT_EDGES', 'o[ - eo]'[, 'w']);Description
Uses Brande’s betweenness centrality algorithm to calculate closeness and betweenness centrality for vertices and betweenness centrality for edges.
Let \(d(s, t)\) denote the distance from \(s \in V\) to \(t \in V\), i.e., the minimum length of all paths connecting \(s\) to \(t\). We have \(d(s, s) = 0\) for all \(s \in V\).
Let \(\sigma_{st}\) denote the number of shortest paths from \(s \in V\) to \(t \in V\) and set \(\sigma_{ss}=1\) by convention. Let \(\sigma_{st}(v)\) denote the number of shortest paths from \(s\) to \(t\) containing \(v \in V\).
We have the following definitions for vertices:
Betweenness centrality for edges is defined similarly.
A high closeness centrality score indicates that a vertex can reach other vertices on relatively short paths; a high betweenness centrality score indicates that a vertex lies on a relatively high number of shortest paths.
All centrality scores are normalized.
But this normalization depends on the graph being connected.
Use ST_ConnectedComponents
to make sure you're calling ST_GraphAnalysis on a
single (strongly) connected component.
A few caveats.
Results will not be accurate if the graph:
- contains "duplicate" edges (having the same source, destination and weight)
- is disconnected. If all closeness centrality scores are zero, this is why.
Though Brande's algorithm is much faster than a naïve approach, it still requires an augmented version of Dijkstra's algorithm to be run starting from each vertex. Thus, calculation times can be rather long for larger graphs.
Input parameters
| Variable | Meaning |
|---|---|
INPUT_EDGES |
Table containing integer columns EDGE_ID, START_NODE and END_NODE; and optionally a weight column w (if the graph is weighted) and/or an edge orientation column eo (required if global orientation is not undirected) |
o |
Global orientation string: directed, reversed or undirected |
eo |
Edge orientation column name indicating individual edge orientations: 1 (directed), -1 (reversed) or 0 (undirected); required if global orientation is directed or reversed |
w |
Edge weights column name |
Screenshots
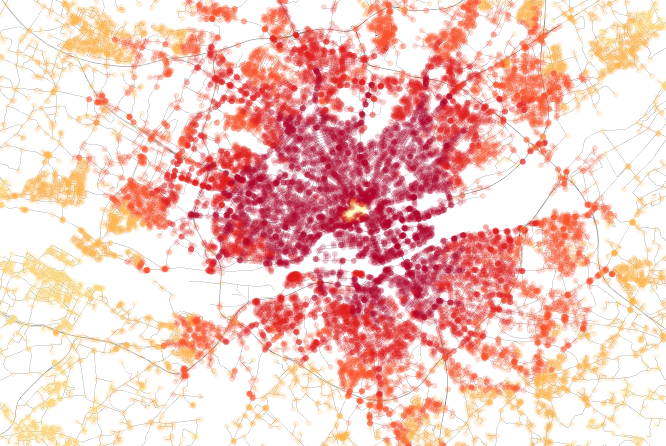
Closeness centrality of Nantes, France. Notice the limited traffic zone in the center.
Edge betweenness centrality of Nantes, France. Notice how the beltway and bridges really stand out.
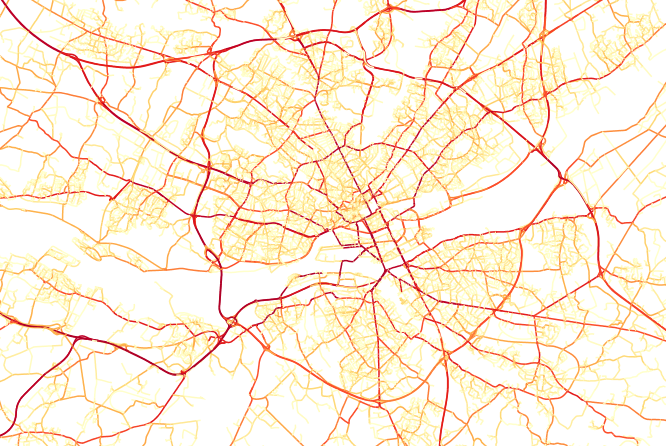
The above screenshots were generated in OrbisGIS.
Examples
-- We will do graph analysis on the largest strongly connected
-- component of the directed weighted graph examined in
-- ST_ShortestPath examples, illustrated below.
SELECT * FROM EDGES_EO_W_SCC;
-- | EDGE_ID | START_NODE | END_NODE | WEIGHT | EDGE_ORIENTATION |
-- |---------|------------|----------|--------|------------------|
-- | 1 | 1 | 2 | 10.0 | 1 |
-- | 2 | 2 | 4 | 1.0 | -1 |
-- | 3 | 2 | 3 | 2.0 | 1 |
-- | 4 | 3 | 2 | 3.0 | 1 |
-- | 5 | 1 | 3 | 5.0 | 1 |
-- | 6 | 3 | 4 | 9.0 | 1 |
-- | 7 | 3 | 5 | 2.0 | 1 |
-- | 8 | 4 | 5 | 4.0 | 1 |
-- | 9 | 5 | 4 | 6.0 | 1 |
-- | 10 | 5 | 1 | 7.0 | 0 |-- Do the graph analysis.
CALL ST_GraphAnalysis('EDGES_EO_W_SCC',
'directed - EDGE_ORIENTATION', 'WEIGHT');
-- The results for nodes:
SELECT * FROM EDGES_EO_W_SCC_NODE_CENT;
-- | NODE_ID | BETWEENNESS | CLOSENESS |
-- |---------|--------------------|---------------------|
-- | 1 | 0.0 | 0.12121212121212122 |
-- | 2 | 0.3333333333333333 | 0.14814814814814814 |
-- | 3 | 0.8333333333333334 | 0.18181818181818182 |
-- | 4 | 0.3333333333333333 | 0.21052631578947367 |
-- | 5 | 1.0 | 0.13793103448275862 |
-- We use linear interpolation from red (0) to blue (1) to
-- illustrate node betweenness.
SELECT NODE_ID,
BETWEENNESS,
CAST(255*(1-BETWEENNESS) AS INT) RED,
CAST(255*BETWEENNESS AS INT) BLUE
FROM EDGES_EO_W_SCC_NODE_CENT
ORDER BY BETWEENNESS DESC;
-- | NODE_ID | BETWEENNESS | RED | BLUE |
-- |---------|--------------------|---------------------|------|
-- | 5 | 1.0 | 0 | 255 |
-- | 3 | 0.8333333333333334 | 42 | 213 |
-- | 4 | 0.3333333333333333 | 170 | 85 |
-- | 2 | 0.3333333333333333 | 170 | 85 |
-- | 1 | 0.0 | 255 | 0 |-- We use linear interpolation from red (0) to blue (1) to
-- illustrate closeness.
SELECT NODE_ID,
CLOSENESS,
CLOSE_INTERP,
CAST(255*(1-CLOSE_INTERP) AS INT) RED,
CAST(255*CLOSE_INTERP AS INT) BLUE
FROM (SELECT NODE_ID,
CLOSENESS,
(CLOSENESS - (SELECT MIN(CLOSENESS)
FROM EDGES_EO_W_SCC_NODE_CENT)) /
((SELECT MAX(CLOSENESS)
FROM EDGES_EO_W_SCC_NODE_CENT) -
(SELECT MIN(CLOSENESS)
FROM EDGES_EO_W_SCC_NODE_CENT))
AS CLOSE_INTERP
FROM EDGES_EO_W_SCC_NODE_CENT)
ORDER BY CLOSENESS DESC;
-- |NODE_ID | CLOSENESS | CLOSE_INTERP |RED |BLUE |
-- |--------| --------------------|---------------------|----|-----|
-- | 4 | 0.21052631578947367 | 1.0 | 0 | 255 |
-- | 3 | 0.18181818181818182 | 0.6785714285714287 | 82 | 173 |
-- | 2 | 0.14814814814814814 | 0.3015873015873015 |178 | 77 |
-- | 5 | 0.13793103448275862 | 0.18719211822660095 |207 | 48 |
-- | 1 | 0.12121212121212122 | 0.0 |255 | 0 |-- The results for edges:
SELECT * FROM EDGES_EO_W_SCC_EDGE_CENT ORDER BY BETWEENNESS DESC;
-- | EDGE_ID | BETWEENNESS |
-- |---------|---------------------|
-- | 7 | 1.0 |
-- | 9 | 0.8571428571428571 |
-- | 3 | 0.8571428571428571 |
-- | 10 | 0.5714285714285714 |
-- | 2 | 0.5714285714285714 |
-- | 5 | 0.42857142857142855 |
-- | 4 | 0.2857142857142857 |
-- | 8 | 0.2857142857142857 |
-- | -10 | 0.14285714285714285 |
-- | 1 | 0.0 |
-- | 6 | 0.0 |
-- We use linear interpolation from red (0) to blue (1) to
-- illustrate node betweenness.
SELECT EDGE_ID,
BETWEENNESS,
CAST(255*(1-BETWEENNESS) AS INT) RED,
CAST(255*BETWEENNESS AS INT) BLUE
FROM EDGES_EO_W_SCC_EDGE_CENT
ORDER BY BETWEENNESS DESC;
-- | EDGE_ID | BETWEENNESS | RED | BLUE |
-- |---------|---------------------|-----|------|
-- | 7 | 1.0 | 0 | 255 |
-- | 3 | 0.8571428571428571 | 36 | 219 |
-- | 9 | 0.8571428571428571 | 36 | 219 |
-- | 2 | 0.5714285714285714 | 109 | 146 |
-- | 10 | 0.5714285714285714 | 109 | 146 |
-- | 5 | 0.42857142857142855 | 146 | 109 |
-- | 4 | 0.2857142857142857 | 182 | 73 |
-- | 8 | 0.2857142857142857 | 182 | 73 |
-- | -10 | 0.14285714285714285 | 219 | 36 |
-- | 1 | 0.0 | 255 | 0 |
-- | 6 | 0.0 | 255 | 0 |Exercises
- Use
ST_ShortestPathTreeto calculate the shortest path trees for nodes 1 through 5. Then use the definition of node betweenness to calculate betweenness by hand and verify the results above. - Make use of
ST_ShortestPathto write a script that calculates node betweenness automatically without usingST_GraphAnalysis. Make sure you get the same results as above. - Repeat exercise 2 using
ST_ShortestPathLengthto verify node closeness.
